このブログ記事は、以前書いた記事の続きです。できれば、まずはそちらをお読みください。

Keras/TensorFlowでDNNな囲碁の評価関数を作ってみる
http://www.perfectsky.net/blog/?p=350

ずいぶん長い間ほったらかしにしていたのですが、そろそろ自分でも、囲碁の思考エンジンを作ってみたいと思い、ここ最近、久しぶりに以前作っていたディープラーニングな評価関数の作成の続きをやっています。

ただ、思いつくことはある程度、前回の時に試していたこともあって、ほとんどの試行はたいした改良に繋がらないのですが、その中で唯一、非常に大きく数字が改善したのが、Squeeze-and-Excitation Networks(SENet)というやつです。

[1709.01507] Squeeze-and-Excitation Networks
https://arxiv.org/abs/1709.01507

このモデルがどのようなものかを解説するのは、私にはちょっと難しいので、詳しくはリンク先を読んでいただくとして、以下簡単に、私が試してみたテスト内容とその結果を書いてみたいと思います。

現在、最終的にはクライアントサイドで思考エンジンが動くウェブアプリの制作を目標にしていて、その関係もあって、とりあえず今回は9路盤です。データの作成方法などは前回とほぼ一緒。対称形に8倍して切りの良い数字にまで少し減らして、230万局面分。95%を学習用に、5%を検証用に使います。

NNのモデルは、基本的に、前回の最後の方で使っていた普通のResNetみたいなのが性能良いのでは、と思っているのですが、今回は非力なスマホなどでも動かしたいので、できるだけ小さなモデルにしなければいけません。特に、パラメータ数は、モデルのファイルサイズになってネットワークの転送量とかにまで影響してくるので、少ないにこしたことはないように思います。ということで、Residual Block内は1×1 -> 3×3 -> 1×1のいわゆるBottleneckアーキテクチャにしました。そもそも、たかだか19×19の囲碁で、3×3のConvが30も50も重なるのって、なんかおかしいような気が以前からしていて、なんというか、そんな遠くの場所よりも、まずはもっと近いところとの関係をよく見ないといけないのではと、つい思ってしまうんですよね… 9路盤なんか、たった4つの3×3のConvで、天元のところにすべての座標の入力の情報が来るわけで、そういう意味でも、3×3を一定量1×1に置き換えるのは、理にかなっているような気がしています。「5×5は3×3が2つの方が良いように、3×3はdepthwiseとpointwiseに分けたほうが良い」みたいなことを言われてしまうと、確かに3×3のConvはちょっと大きすぎですよね… 囲碁だったら、四隅の欠けた3×3の、「十字型」なんかどうなんでしょうか？

ってすみません。話がそれてしまいました。元に戻って今回のNNのモデルですが、前回からの変更点としてもうひとつ、入力層の所でまず、周囲をゼロパディングして、9×9だったフィールドを13×13に広げています。これはパラメータ増やさず、ロスを下げます。やっぱり9×9って小さすぎるんですよね、ってまた似たような話に…(笑)

入力は、「手番のプレーヤーの石の配置」、「相手の石の配置」、「コウで打てない場所」、「全部1」の4面(9,9,4)です。最後の「全部1」と、先ほどの入力層でのゼロパディングで、盤上/盤外を表現したつもりです。

その他の条件は、だいたい前回と同じかな？

コードはこんな感じ。まずは「SENetなし」。

BOARD_SIZE = 9
FIELD_SIZE = 13


def rn_block(input):

    relu_1 = Activation("relu")(input)
    bn_1   = BatchNormalization()(relu_1)
    conv_1 = Conv2D(32, (1, 1))(bn_1)

    relu_2 = Activation("relu")(conv_1)
    bn_2   = BatchNormalization()(relu_2)
    conv_2 = Conv2D(32, (3, 3), padding='same')(bn_2)

    relu_3 = Activation("relu")(conv_2)
    bn_3   = BatchNormalization()(relu_3)
    conv_3 = Conv2D(128, (1, 1))(bn_3)

    return conv_3


input = Input(shape=x_train.shape[1:])

main    = ZeroPadding2D(padding=(int((FIELD_SIZE-BOARD_SIZE)/2), int((FIELD_SIZE-BOARD_SIZE)/2)))(input)
rn_fork = Conv2D(128, (3, 3), padding='same')(main)

main    = rn_block(rn_fork)

rn_fork = add([main, rn_fork])

main    = rn_block(rn_fork)

rn_fork = add([main, rn_fork])

main    = rn_block(rn_fork)

rn_fork = add([main, rn_fork])

main    = rn_block(rn_fork)

rn_fork = add([main, rn_fork])

main    = rn_block(rn_fork)

rn_fork = add([main, rn_fork])

main    = rn_block(rn_fork)

main    = add([main, rn_fork])

main    = Activation("relu")(main)
main    = BatchNormalization()(main)
main    = Conv2D(1, (3, 3), padding='valid')(main)
main    = AveragePooling2D(pool_size=(FIELD_SIZE-2, FIELD_SIZE-2))(main)

output  = Flatten()(main)

そして「SENetあり」。

BOARD_SIZE = 9
FIELD_SIZE = 13


def rn_block(input):

    relu_1 = Activation("relu")(input)
    bn_1   = BatchNormalization()(relu_1)
    conv_1 = Conv2D(32, (1, 1))(bn_1)

    relu_2 = Activation("relu")(conv_1)
    bn_2   = BatchNormalization()(relu_2)
    conv_2 = Conv2D(32, (3, 3), padding='same')(bn_2)

    relu_3 = Activation("relu")(conv_2)
    bn_3   = BatchNormalization()(relu_3)
    conv_3 = Conv2D(128, (1, 1))(bn_3)

    return conv_3


def se_block(input):

    ap      = AveragePooling2D(pool_size=(FIELD_SIZE, FIELD_SIZE))(input)
    conv_1  = Conv2D(8, (1, 1))(ap)
    relu    = Activation("relu")(conv_1)
    conv_2  = Conv2D(128, (1, 1))(relu)
    sigmoid = Activation("sigmoid")(conv_2)
    us      = UpSampling2D(size=(FIELD_SIZE, FIELD_SIZE))(sigmoid)

    return us


main    = ZeroPadding2D(padding=(int((FIELD_SIZE-BOARD_SIZE)/2), int((FIELD_SIZE-BOARD_SIZE)/2)))(input)
rn_fork = Conv2D(128, (3, 3), padding='same')(main)

#main    = rn_block(rn_fork)
se_fork = rn_block(rn_fork)
se_out  = se_block(se_fork)
main    = multiply([se_fork, se_out])

rn_fork = add([main, rn_fork])

#main    = rn_block(rn_fork)
se_fork = rn_block(rn_fork)
se_out  = se_block(se_fork)
main    = multiply([se_fork, se_out])

rn_fork = add([main, rn_fork])

#main    = rn_block(rn_fork)
se_fork = rn_block(rn_fork)
se_out  = se_block(se_fork)
main    = multiply([se_fork, se_out])

rn_fork = add([main, rn_fork])

#main    = rn_block(rn_fork)
se_fork = rn_block(rn_fork)
se_out  = se_block(se_fork)
main    = multiply([se_fork, se_out])

rn_fork = add([main, rn_fork])

#main    = rn_block(rn_fork)
se_fork = rn_block(rn_fork)
se_out  = se_block(se_fork)
main    = multiply([se_fork, se_out])

rn_fork = add([main, rn_fork])

#main    = rn_block(rn_fork)
se_fork = rn_block(rn_fork)
se_out  = se_block(se_fork)
main    = multiply([se_fork, se_out])

main    = add([main, rn_fork])

main    = Activation("relu")(main)
main    = BatchNormalization()(main)
main    = Conv2D(1, (3, 3), padding='valid')(main)
main    = AveragePooling2D(pool_size=(FIELD_SIZE-2, FIELD_SIZE-2))(main)

output  = Flatten()(main)

「SENetなし」はResidual Blockが6つと7つの2種類、「SENetあり」はResidual Blockが6つの、計3種類をテストしてグラフにしてみました。

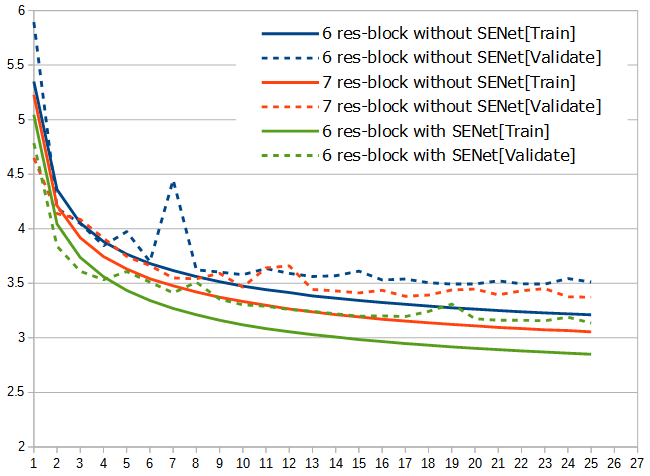
「SENetなし/Residual Block 7つ」と「SENetあり」は、パラメータ数、予測に掛かる時間、1エポックあたりの学習時間などがそれほどは大きく変わらず、それでいてこのロスの差なので、すばらしいです。ILSVRC2017チャンプは伊達ではない(笑)。しばらく忙しいのですぐには無理そうですが、いずれこいつを使って一手全幅君を作ってみたいと思います。

[追記 2018/4/4]
現在使用している学習データのラベルは、Rayに付けてもらったものですが、それをそのデータを学習したDNNで付け替えて、もう一度最初から学習し直したらどうなるのか、試してみました。

学習する局面は上と同じ230万局面分。95%を学習用、5%を検証用に。ネットワーク構成も上のSENetありと基本的に同じで、10 res-blockです。今回の複数のテストでの唯一の違いは学習データのラベルで、まずは次の3種類、

• [1] Train/ValidateともRayが付けたもの
• [2] Trainを[1]の50エポック目のDNNが付け、ValidateはRayが付けたもの
• [3] Train/Validateとも[1]の50エポック目のDNNが付けたもの

です。[3]は[2]とTrainのラベルが同じなので、Validateだけ調べれば良かったのですが、実際にやってみると、想像以上に低い数字が出て来て自分の書いたコードが信用できなくなり(笑)、念のために、いつもと同じように最初から学習回しながら、Validateを計測してみました(どうやら、自分の書いたコードは合ってたみたい…)。乱数の加減も今回はあまり関係無かったようで、赤の実線は緑の実線にきれいに隠れていますが、そこにあります(一応、少し太くしておいた(笑))。

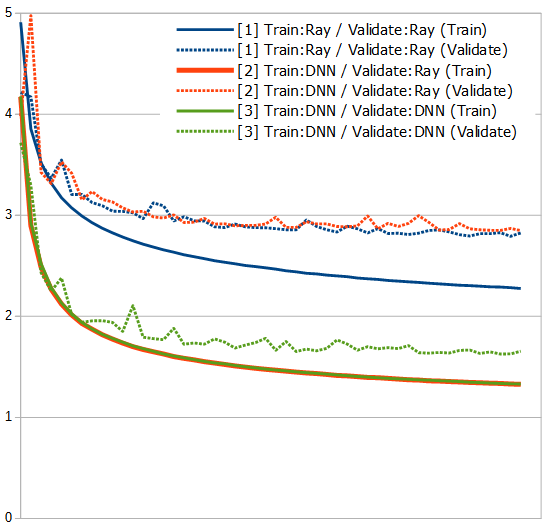
正直、驚きの結果です。DNNに予測させるのは、Rayにラベルを付けてもらうより、遥かにコストが掛かからないので、「もし、DNNが付けたラベルでそれなりに学習できたら、データの水増しが可能になるかも」ぐらいに思っていたのですが、ばっさりと全部差し替えても全く問題なさそうですし、グラフ見ているだけでははっきりしませんが、囲碁の神様が付けたラベルに対して、[1]より[2]/[3]の方が性能が高い可能性までありそうに見えます。しかし、そんなうまい話本当にあるのかなあ？ どうも信じられないのですが…

以前にも書きましたが、同じ局面の対称形をDNNで予測させると、結構ばらばらな数字を返してくるので、

• [4] Trainを[1]の50エポック目のDNNが予測した8対称形すべての平均にして、ValidateはRayが付けたもの

もテストしてみました。

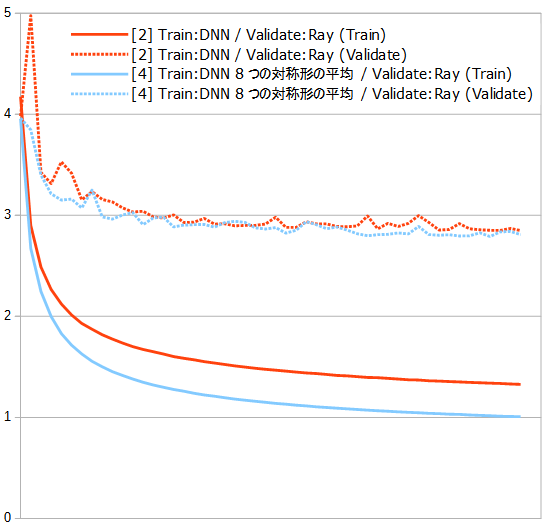
このブログには書いていませんが、以前Trainのラベルに平均0の乱数を混ぜて学習させてみたことがあったのですが、その時も意外とValidateの数字が大きく悪くはなったりせず(もちろんTrainはノイズの分がっつり悪くなります)、たくさんのデータで鍛えるとそんなものなんだなあと思ったことがあったのですが、今回の[2]は、[4]に平均0の乱数を混ぜたようなものなので、似たような結果と言えるでしょうか、ってじゃあやっぱり精度の高い予測が欲しい時は、平均とって使った方が良さそうですね。うーん、めんどくさ…

[追記 2018/4/30]
続きの記事があります。

囲碁の思考エンジンを作ってみる
http://www.perfectsky.net/blog/?p=389